A State-of-the-Art Method for Generating Photo-Realistic Textures in Real Time
Our Zalando Research team give an overview of the latest work in image generation using machine learning.
This blog post gives an overview of the latest work in image generation using machine learning at Zalando Research. In particular, we show how we advanced the state-of-the art in the field by using deep neural networks to produce photo-realistic high resolution texture images in real-time.
In the spirit of Zalando’s embrace of open source, we've published twoconsecutive (see [Jetchev et al. 2016] and [Bergmann et al. 2017]) papers at world-class machine learning conferences, and the source code ( SGAN and PSGAN) to reproduce the research is also available on GitHub.
State-of-the-art in Machine Learning
It’s all over town. Machine learning, and in particular deep learning, is the new black. And justifiably so: not only do vast datasets and raw computational GPU power contribute to this fact, but also the influx of brilliant people dedicating their time to the topic has accelerated the progress in the field.
Computer Vision and Machine Learning
Computer vision methods are very popular in Zalando’s research lab, where we constantly work on improving our classification and recommendation methods. This type of business relevant research aims to discriminate articles according to their visual properties, which is what most people expect from computer vision methods. However, the recent deep learning revolution has made a great step towards generative models - models that can create novel content and images.
Generative Adversarial Networks
The typical approach in machine learning is to formulate a so-called loss function, which basically quantifies a distance of the output of a model to samples from a dataset. The model parameters can then be optimized on this dataset by minimizing a loss function. For many datasets this is a viable approach - for image generation, however, it fails. The problem is that nobody knows how to plausibly measure the distance of a generated image to a real one - standard measures, which typically assume isotropic Gaussianity, do not correspond to our perception of image distances. However, how do humans know how to perceive this distance? Could it be that the answer is in the image data itself?
In 2014, Ian Goodfellow published a brilliant idea [Goodfellow et al. 2014] which strongly indicates that it seems to be in the data: he proposed to learn the loss function in addition to the model. But how can this be done?
The key inspiration comes from game theory. We have two different networks. First, a generative model (‘generator network’) takes noise as input and should transform it into valid images. Second, a discriminator network is added, which should learn the loss function. The two networks then enter a game in which they compete: the discriminator network tries to tell if an image is from the generator network or a real image, while the generator tries to be as good as possible in fooling the discriminator network into believing that it produces real images. Due to the competitive nature of this setup, Ian called this approach Generative Adversarial Networks (GANs).
Since 2014 a lot has happened, in particular GANs have been built with convolutional architectures, called DCGANs (Deep Convolutional GANs) [Radford et al. 2015]. DCGANs are able to produce convincing and crisp images that resemble, but are not contained, in the training set - i.e. to some degree you could say the network is creative, because it invents new images. You could now argue that this is not too impressive, because it is ‘just’ in the style of the training set, and hence not really ‘creative’. However, let us convince you that it is at least technically spectacular.
Consider that DCGANs learn a probability distribution over images, which are of extremely high dimensionality. As an example, assume we want to fit a Gaussian distribution to match image statistics. The sufficient statistic (i.e. the parameters that fully specify it) of a Gaussian distribution is the mean and covariance matrix, which for a color image of (only) 64x64 pixels would mean that more than 75 million parameters have to be determined. To make this even worse, it has been known for decades by now that Gaussian statistics are not even sufficient for images - 75 million parameters are therefore only a lower bound. Hence, as typically less than 75 million images are used, it is from a statistical perspective borderline crazy that DCGANs actually work at all.
Texture synthesis methods
Textures capture the look and feel of a surface, and they are very important in Computer Generated Imagery. The goal of texture synthesis is to learn a generating process and sample textures with the "right" properties, corresponding to an example texture image.
Classical methods include instance-based approaches [Efros et al. 2001] where parts of the example texture are copied and recombined. Other methods define parametric statistics [Portilla et al. 2000] that capture the properties of the “right” texture and create images by optimizing a loss function to minimize the distance between the example and the generated images.
However, both of these methods have a big drawback: they are slow to generate images, taking as much as 10 minutes for a single output texture of size 256x256. This is clearly too slow for many applications.
More recent work [Gatys et al. 2015] uses filters of pretrained deep neural networks to define powerful statistics of texture properties. It yields textures of very high quality, but it comes with the disadvantage of high computational cost to produce a novel texture, due to the optimization procedure involved (note that there has been work to short-cut the optimization procedure more recently).
Besides the computational speed issue, there are a few other issues plaguing texture synthesis methods. One of them is the failure to accurately reproduce textures with periodic patterns. Such textures are important both in nature -- e.g. the scales of a fish -- and for human fashion design, e.g. the regular patterns of a knitted material. Another issue needing improvement is the ability to handle multiple example textures and learning a texture process with properties reflecting the diverse inputs. The methods mentioned above cannot flexibly model diverse texture classes in the process they learn.
Spatial Generative Adversarial Networks (SGANs)
Our own research into generative models and textures allowed us to solve many of the challenges of the existing texture synthesis methods and constitute a new state of the art for texture generation algorithms.
The key insight we had in Spatial Generative Adversarial Networks (SGANs) [Jetchev et al. 2016] is that in texture images, the appearance is the same everywhere. Hence, a texture generation network needs to reproduce the data statistics only locally, and, when we ignore alignment issues (see PSGAN below for how to fix this), can generate far-away regions of an image independent of each other. But how can this idea be implemented in a GAN?
Recall that in GANs a randomly sampled input vector, e.g. from a uniform distribution, gets transformed into an image by the generative network. We extend this concept to sampling a whole tensor Z, or spatial field of vectors. This tensor Z is then transformed by a fully convolutional network to produce an image X. A fully convolutional network consists of exclusively convolutional layers, i.e. layers in which neuronal weights are shared over spatial positions. The images this network produces have therefore local statistics that are the same everywhere.

Figure 1: The left column shows images used to train the SGAN algorithm. The algorithm analyses the structure in these images and then can produce arbitrary large images with the same texture as in the input images. The results are shown in the right column.

Figure 2: In the left column several images are provided to train the SGAN algorithm. The output on the right side then mixes properties of the input images in such a way that the output contains properties of all images smoothly interpolated. While this is a nice property of SGANs, it is not in general desirable (PSGAN improves this by allowing sampling of different textures). The top row example mixed 10000 different flowers for the final result, of which only 3 are shown top left.
In a standard, non-convolutional fully-connected network, the addition of new neurons at a layer implies the addition of weights that connect to this neuron. In a convolutional layer, this is not the case, as the weights are shared across positions. Hence, the spatial extent of a layer can be changed by simply changing the inputs to the layer. In a fully-convolutional network, a model can be trained on a certain image size, but then rolled-out to a much larger size. In fact, given the texture assumption above, i.e. that the generation process of the image at different locations is independent (given a large enough distance), generation of images of arbitrary larger size is possible. The only (theoretical) constraint is computation time. These resulting images locally resemble the texture of the original image on which the model was trained, see Figure 1. This is a key point where the research goes beyond the literature, as standard GANs are bound to a fixed size, and producing globally coherent, uncannily large images remains a standing challenge.
Further, as the generator network is a fully-convolutional feed-forward network, and convolutions are efficiently implemented on GPUs and in current deep learning libraries, image generation is very fast: generation of an image of size 512x512 takes 0.019 seconds on an nVidia K80 GPU. This corresponds to 50 frames per second! As this is real-time speed, we built a webcam demo, with which you can observe and manipulate texture generation – see here.
Periodic Spatial GANs (PSGANs)
The second paper we wrote on the texture topic was published recently at the International Conference of Machine Learning, where we also gave a talk about it. In the paper, we improved two shortcomings of the original SGAN paper.

Figure 3: Shown are 4 times 3 tiles of generated textures from a Periodic Spatial GAN - PSGAN. Within the tiles the global dimensions of the generating tensor are set to be identical, yet random in each tile. Local dimensions are random everywhere. The complete resulting tensor Z is then passed through the generator network, and in a single feed-forward sweep yields the complete image.
The first shortcoming of SGANs is that they always sample from the same statistical process, which means that after they’re trained, they always produce the same texture. When the network is trained on a single image, it produces texture images that correspond to the texture that was in this image. However, if it was trained on a set of images, it produces a texture image that mixes the original texture images in a single texture in the outputs, see Figure 2. Often, though, we’d rather want a network to produce an output image, which resembles one of the training images - and not all simultaneously. This means that the generation process needs to have some global information, that encodes which texture to generate. We achieved this by setting a few dimensions of each vector in the spatial field of vectors Z to be identical across all positions - instead of randomly sampling it as in the previous section. These dimensions are hence globally identical, and we therefore call them global dimensions. Figure 3 shows an image that resulted from a model trained with this idea on many pictures of snake skins from the Describable Textures Dataset. Figure 4 shows how the flower example looks when explicitly learning the diverse flower image dataset, and that this is totally different behaviour than the example in Figure 2. In addition to training on a set of texture images, the model can also be trained on clip-outs of one larger image, which itself does not have to be an image of textures. Generating images with the model will then result in textures that resemble the local appearance of the original image.

Figure 4: 3x3 tiles from the Flower dataset, illustrating how PSGAN can automatically detect the various types of input images it gets, and can learn a texture generating process that flexibly represents these distinct different texture examples.
An interesting property of GANs is that a small change in the input vector Z results in a small change of the output image. Moving between two points in Z-space hence morphs one image smoothly into another one [Radford et al. 2015]. In our model, we can take this property one step further, because we have a spatial field of inputs: we can interpolate the global dimension in Z in space. Figure 5 shows that this produces smooth transitions between the learned textures in one image.

Figure 5: Illustration of the learned “manifold” property of the PSGAN. The system is trained on a whole set of DTD snake skins. Simple interpolation in the global variables of the Z-tensor yields an output image that smoothly morphs between textures (here 4 independent ones are sampled in the four corners of the image). Note that the texture looks locally plausible everywhere.
Second, many textures contain long-range dependencies. In particular, in periodic textures the structure changes at well-defined length scales - the periods - thus the generation process is not independent of other positions. However, we can make it independent by handing information about the phase of our periodic structure to the local generation processes. We did this by adding simple sinusoids of a given periodicity, so-called plane-waves (see Figure 6), to our input Z. The wavenumbers that determine the periodicity of the sinusoids were learned as a function of the current texture (using multi-layer perceptrons), i.e. as a function of the global dimensions. This allows the network to learn different periodic structures for diverse textures. Figure 7 shows generated images learned on two different input images for various methods: text and a honeycomb texture. PSGAN is the only method which manages to generate images without artifacts. Note in particular that the other two neural based methods (SGAN and Gatys’ method) scramble the honeycomb pattern. Interestingly, our simulations indicate that the periodic dimensions also helped stabilize the generation process of non-periodic patterns. Our interpretation of this observation is that it helps to anchor generation processes to a coordinate system.

Figure 6: Transforming a coordinate system with sinusoidal functions with learned wavenumbers allows to flexibly learn planar waves and represent periodical patterns accurately.
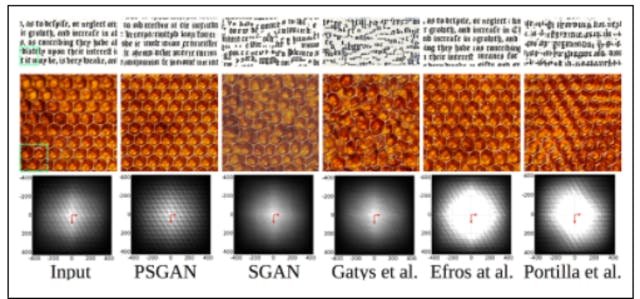
Figure 7: This figure illustrates the superior ability of the PSGAN to handle periodic textures. Other methods either fail completely, or have occasional artifacts (Efros et al.), while PSGAN produces globally coherent periodic textures.
Discussion and Outlook
As a wrap-up, in this blog post we have given an overview of how we extended current methods in generative image modeling to allow for very fast creation of high-resolution texture images.
The method exceeds the state-of-the art in the following ways:
- Scalable, arbitrary large texture image generation
- Learn texture image processes representing various texture image classes
- Flexibly sample diverse textures and blend them in novel textures
Please check out our research papers for more details, and these videos as examples that show you how to animate textures:
So far, this is basic research with a strong academic focus. In the more long term perspective, one of several potential products could be a virtual wardrobe, which could be used to asses how Zalando’s customers will look in a desired article, e.g. a dress. Will it fit? How will I look in it? Solutions to these questions will very likely become a reality in the future of e-commerce online shopping. We already have academic results that get closer to this use case and a paper will be published soon in a workshop of “Computer Vision for Fashion” at the International Conference for Computer Vision.
Stay tuned!
References
[Bergmann et al. 2017] Urs Bergmann and Nikolay Jetchev and Roland Vollgraf.
Learning Texture Manifolds with the Periodic Spatial GAN. Proceedings of The 34th International Conference on Machine Learning, ICML 2017.
[Efros et al. 2001] Alexei A. Efros and William T. Freeman. Image quilting for texture synthesis and transfer. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH, 2001.
[Gatys et al. 2015] Leon Gatys, Alexander Ecker, and Matthias Bethge. Texture synthesis using convolutional neural networks. In Advances in Neural Information Processing Systems 28, 2015.
[Goodfellow et al. 2014] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron C. Courville, and Yoshua Bengio. Generative adversarial nets. In Advances in Neural Information Processing Systems 27, 2014.
[Jetchev et al. 2016] Nikolay Jetchev, Urs Bergmann and Roland Vollgraf. Texture Synthesis with Spatial Generative Adversarial Networks. Adversarial Learning Workshop at NIPS 2016
[Portilla et al. 2000] Javier Portilla and Eero P. Simoncelli. A parametric texture model based on joint statistics of complex wavelet coefficients. Int. J. Comput. Vision, 40(1), October 2000.
[Radford et al. 2015] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015.
We're hiring! Do you like working in an ever evolving organization such as Zalando? Consider joining our teams as a Applied Scientist!










